Ramsey Theorems in Euclidean Geometry
By Kevin Santos
Published March 14, 2022
In this article, I will give a very brief overview of Ramsey theory and some of its main theorems. I will go over an application of Ramsey’s Theorem in Euclidean geometry, and I will also define a Ramsey property and describe whether certain geometrical objects satisfy it.
To motivate this discussion, consider the following theorem. It states that if we have a group of six people, the group is big enough to guarantee the existence of a certain subset of people among them.
Theorem 1. Theorem on Friends and Strangers. Among six people, there must be three mutual acquaintances (three people who are all acquainted with each other) or three mutual strangers (three people who have all never met each other). If there are only five people, however, there may not be a set of three mutual acquaintances or three mutual strangers.
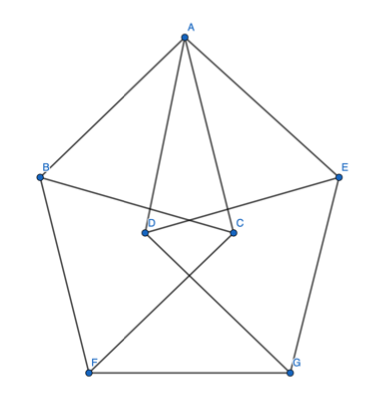
This theorem can be restated in terms of graph theory: suppose we have a graph with six vertices and each vertex is connected to the other five, so that each pair of distinct vertices has an edge between them (this is a complete graph on six vertices; see Fig. 2). If we assign each edge one of two colours, red or blue, there must always be a triangle whose edges are all the same colour, no matter how we choose to colour the edges (see [1]). However, if the graph only has five vertices, we can’t guarantee the existence of a triangle with all edges the same colour. The proof is covered in the accompanying video and in Fig. 2 and Fig. 3.
1 Ramsey’s theorem and Ramsey numbers
F.P. Ramsey first proved the theorem that now bears his name, which roughly states that it is always possible to make a set large enough to guarantee that it contains certain ordered subsets. The following is a finite version of Ramsey’s theorem, found in [2]. (Note: the theorem is also true in the analogous case with more than two colours.)
Theorem 2. Ramsey’s Theorem. Let m, n, and k be positive integers. Then there exists a positive integer
that satisfies the following property. For any set S of size N (or greater), consider the family of k-element subsets of S. If we assign each of these subsets one of two colours, say red and blue, then there is either a subset of S with m elements whose k-subsets are all red, or a subset of S with n elements whose k-subsets are all blue.
For example, Theorem 1 states that if we have a complete graph on six vertices and we colour its edges red or blue, we can guarantee the existence of a triangle with all edges the same colour. If we associate each edge with its two endpoints, we can think of each edge as a 2-element subset of the set of vertices. Then Theorem 1 says that R2 (3, 3) = 6. That is, if we have 6 vertices and we assign each of the 2-element subsets a colour by colouring the edge between them red or blue, then we can always find a 3-element subset whose edges are all red, or a 3-element subset whose edges are all blue. However, this isn’t guaranteed if we only have 5 vertices, so 6 is the minimum number for which this property holds. Hence, R2(3, 3) = 6.
The main concern of Ramsey theory involves searching for ordered substructures within larger structures and determining how large the structure needs to be in order to guarantee that these ordered sets exist. Mathematicians have tried to determine values or bounds for Ramsey numbers Rk(m,n), generating many open problems that have yet to be solved.
Ramsey theory is considered a branch of combinatorics, and while it has its origins in logic and graph theory, we can use Ramsey’s theorem to prove statements about geometrical objects, as in the following theorem by Erd ̋os and Szekeres, whose proof is detailed in [2]. [3] contains additional proofs of this theorem.
Theorem 3. For a given integer n, there exists an integer N such that any N points on the plane (where no three are collinear) will contain n points that form a convex n-gon.
A polygon is convex if any line segment connecting any two of its vertices is contained inside the polygon. The proof of this theorem follows directly from these two lemmas, combined with Ramsey’s theorem.
Lemma 1. For any set of five points in the plane (no three points collinear), four must form the vertices of a convex quadrilateral.
Lemma 2. If all the quadrilaterals formed from a set of n points (no three points collinear) are convex, then the n points form a convex n-gon.
Taking the above lemmas as given (their proofs can be found in [2]), we can then apply Ramsey’s theorem to prove Theorem 3.
Proof. Let n be a given integer, and let N be the integer given by Ramsey’s theorem, N = R4(n,5). That is, Ramsey’s theorem guarantees that there is a number N large enough that satisfies the following: for any set of size N or greater, if we colour each of the 4-element subsets red or blue, there is either a subset with n elements whose 4-element subsets are all red, or a subset with 5 elements whose 4-element subsets are all blue. We will show that for any set of N points on the plane, there must be a subset of n points that form a convex n-gon.
Take an arbitrary set of N points in the plane, and consider its 4-element subsets. For each 4-element subset, colour it red if it forms a convex quadrilateral and colour it blue if it forms a convex quadrilateral. By Ramsey’s theorem and the choice of N = R4 (n, 5), we can guarantee the existence of either a subset of n points whose 4-element subsets are all red, or a subset of 5 points whose 4-element subsets all blue. That is, there must be a set of n points whose quadrilaterals are all convex, or a set of 5 points whose quadrilaterals are all concave. By Lemma 1, the second situation is impossible, since if we have 5 points, there must be 4 points among them that form a convex quadrilateral. Therefore, we must have a set of n points whose quadrilaterals are all convex. By Lemma 2, these n points form a convex n-gon.
The problem of what exactly this N is for a given n has yet to be solved. (Ramsey’s theorem says that such an N exists, but it doesn’t give a value of N.) It’s been conjectured that for a given n, the corresponding N promised by Theorem 2 would be N = 2n−2 + 1, but mathematicians have only been able to find upper and lower bounds for N. See [3] for a survey of the current progress in the search for Ramsey numbers.
2 A Ramsey property
We can also ask whether certain geometrical objects satisfy a Ramsey property, described as follows.
In this article, I will only consider objects in two-dimensional Euclidean space (E2). The following definition and notations are adapted from [4]. Let K be a finite set of points in E . An r-colouring of the Euclidean plane is a map where we assign each of the points in E2 to one of r colours. A set S is monochromatic if each point in S is assigned the same colour. If, for any r-colouring of E2, there is a monochromatic set of points K where K is congruent to K, we say that K is r-Ramsey and write E −→ K. Otherwise, if we can show that there exists an r-colouring where there are no monochromatic sets congruent to K, we write E ̸−→ K. (There are many different notations used in the literature to denote r-Ramsey sets, including K → (E2)r, K < (E2)r, “R(K,E2,r) is true”, and so on.)
Theorem 4. Let P be a pair of points distance 1 apart. Then E −→ P . In other words, no matter how we colour the points on the plane with 2 colours, we can always find two points of the same colour distance 1 apart. Similarly, E −→ P .
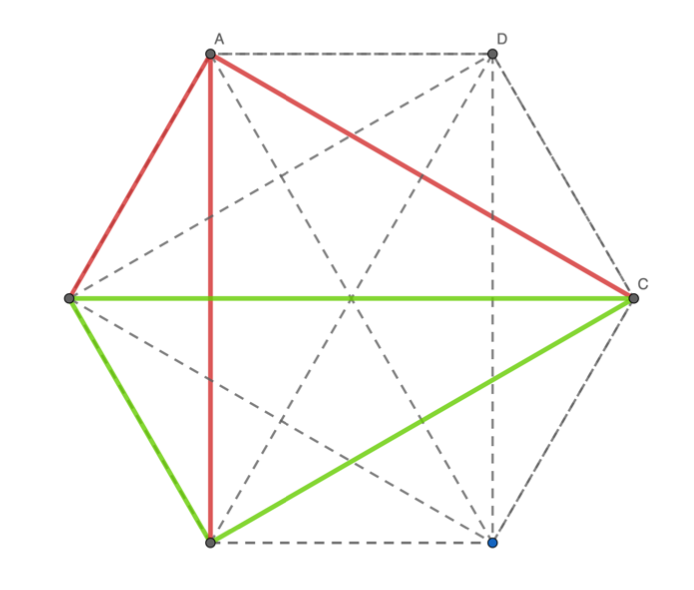
Proof. The proof will be explained in the video, but it can be deduced by considering Fig. 1. In the diagram, each point is distance 1 apart from its connected neighbours, and we can show that there must be two adjacent points with the same colour using a proof by contradiction.
After pairs of points, we can consider triangles. For a given triangle, is it always possible to find a monochromatic congruent triangle for any given colouring?
Figure 1: Any 2- or 3- colouring contains a pair of points distance 1 apart with the same colour.
Theorem 5.
The above theorem can be found in [5]. It’s a direct corollary of the following two lemmas, adapted from [5], which are proven in the accompanying video. Their proofs use similar ideas to the proof of Theorem 4.
Lemma 3. Let T be a triangle in E with side lengths x, y, and z and consider a given 2-colouring of E . If there is a monochromatic equilateral triangle with a side length of either x, y, or z, then there exists a monochromatic triangle congruent to T.
Lemma 4. For any given 2-colouring of the plane, we can always find at least one monochromatic equilateral triangle whose side length is one of:
It has been shown that many types of triangles are 2-Ramsey, and it is conjectured that for any 2- colouring of the plane, we should be able to find monochromatic triangles congruent to any given triangle (with the possible exception of a single equilateral triangle), but this has yet to be proven [4]. There are colourings that can avoid a specific equilateral triangle; consider the following partition of the plane:
This colours the plane into alternating half-open strips and prevents the possibility of any monochromatic equilateral triangle with side length √ 3.
3 Extensions
We can extend these problems further by generalizing to higher-dimensional Euclidean space. For example, it can be shown that for any set of three points
That is, if we colour each point in E3 using two colours, we can always find a monochromatic set congruent to any given set of three points. We can also identify Ramsey sets by considering higher dimensions; a set K is Ramsey (not just r-Ramsey) if, for any r, there exists an N sufficiently large that satisfies
[4] has some examples of Ramsey sets.
We can also consider transformations on the space. We can consider whether the property
holds, where T(K) represents the image of K under a certain transformation or group of transformations.
Most of the current work in Ramsey theory is centered around finding Ramsey numbers; for example, while the exact values of R2(3,3) and R2(4,4) are known (R2(3,3) = 6 and R2(4,4) = 18), R2(5,5) has yet to be found [4]. Going back to the first example, this means we need a group of at least 18 people to guarantee that there are either 4 mutual acquaintances or 4 mutual strangers, but we don’t know exactly how big a group of people needs to be in order to guarantee there are either 5 mutual acquaintances or 5 mutual strangers. Like many open problems in math, it’s a problem that can be easily formulated, but still hasn’t been solved.
Figure 2: Consider any point and the five edges leading from it. By the pigeonhole principle, since there are five edges and two colours, we know at least three of those edges must be the same colour, say red. Then consider the edges connecting the endpoints of those three edges, marked as green. If at least one of those edges is red, we will have a red triangle. Otherwise, if all those edges are blue, those three edges will form a blue triangle. In any case, there must be either a red or blue triangle.
Figure 3: This is a way of colouring red and blue edges in a complete graph on five vertices that does not contain a red or blue triangle.
References
[1] A. Bogomolny, “Party Acquaintances.” [Online]. Available: http://www.cut-the- knot.org/Curriculum/Combinatorics/ThreeOrThree.shtml
[2] J. Marshall Hall, “Ramsey’s Theorem,” in Combinatorial Theory. John Wiley & Sons, Ltd, 1988, pp. 73–76. [Online]. Available: http://onlinelibrary.wiley.com/doi/abs/10.1002/9781118032862.ch6
[3] W. Morris and V. Soltan, “The Erdos-Szekeres problem on points in convex position – a survey,” Bulletin of the American Mathematical Society, vol. 37, no. 4, pp. 437–458, 2000. [Online]. Available: http://www.ams.org/bull/2000-37-04/S0273-0979-00-00877-6/
[4] J. E. Goodman and J. O’Rourke, Handbook of discrete and computational geometry, 2nd ed., ser. Discrete mathematics and its applications. Boca Raton: Chapman & Hall/CRC, 2004.
[5] P. Erd ̈os, R. L. Graham, P. Montgomery, B. L. Rothschild, J. Spencer, and E. G. Straus, “Euclidean ramsey theorems. I,” Journal of Combinatorial Theory, Series A, vol. 14, no. 3, pp. 341–363, May 1973. [Online]. Available: https://www.sciencedirect.com/science/article/pii/0097316573900113